Schedule of GdR MOA 2022 workshop
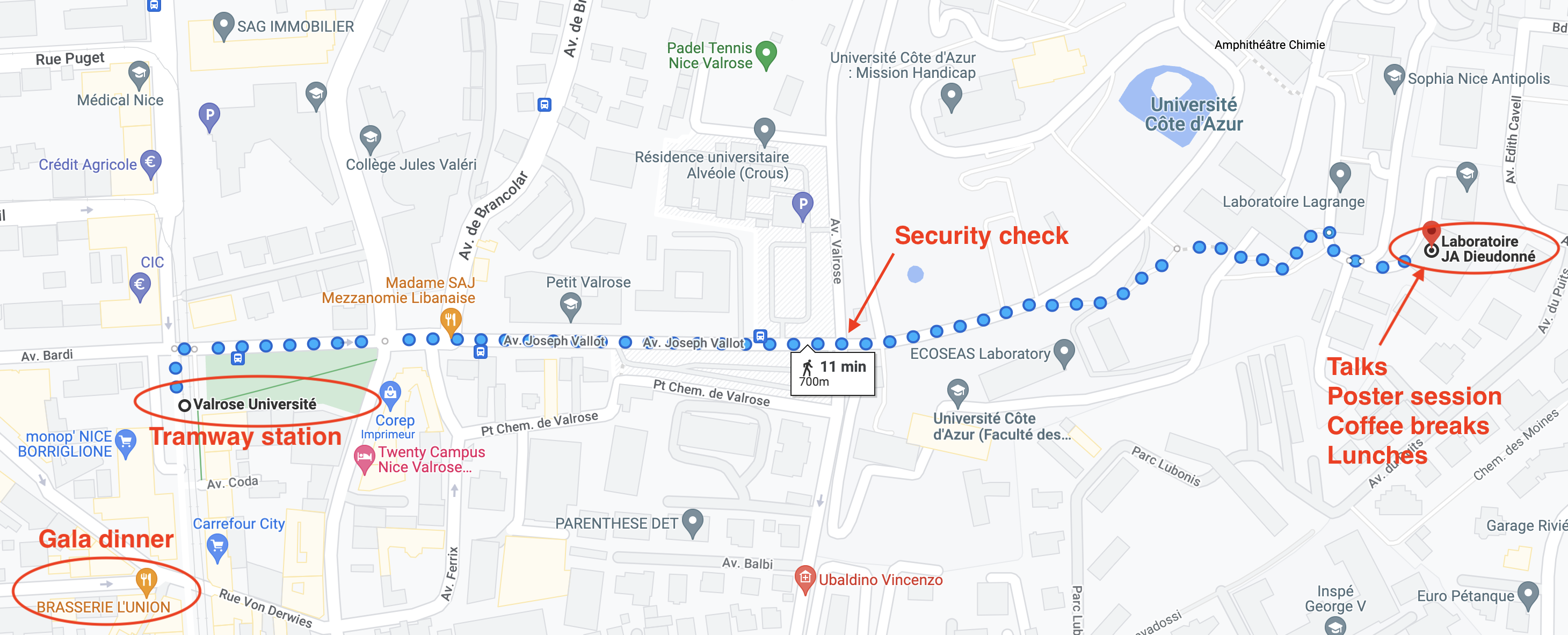
Every lectures and talks will take place in Salle de conférence du Laboratoire J.A. Dieudonné. Coffee breaks and lunches are provided on-site (as buffet).
Tuesday, October 11th, 2022 (Mini-course only)
01:30pm – 02:00pm: Welcome at Université Côte d'Azur, Laboratoire J.A. Dieudonné
02:00pm – 03:30pm: Mini-Course
Title : Fast Algorithmic Methods for Optimization and Learning (abstract)
Instructors:
- Samir Adly (Université de Limoges)
- Hedy Attouch (Université de Montpellier), slides
03:30pm – 04:00pm: Coffee break
04:00pm – 05:30pm: Mini-Course
Title : Fast Algorithmic Methods for Optimization and Learning (abstract)
Wednesday, October 12th, 2022 (Mini-course & Workshop)
09:00am – 10:30am: Mini-Course
Title : Fast Algorithmic Methods for Optimization and Learning (abstract)
10:30am – 11:00am: Coffee break
11:00am – 12:30am: Mini-Course
Title : Fast Algorithmic Methods for Optimization and Learning (abstract)
12:30pm – 01:30pm: Lunch time
Buffet for mini-course attendeees at Laboratoire J.A. Dieudonné
01:30pm – 02:00pm: Welcome at Université Côte d'Azur, Laboratoire J.A. Dieudonné
02:00pm – 03:00pm: Andrea Walther (HU Berlin)
03:00pm – 03:30pm: Tam Le (Toulouse School of Economics)
03:30pm – 05:00pm: Poster session with coffee break (Room 1)
05:00pm – 05:30pm: Sorin-Mihai Grad (ENSTA Paris)
05:30pm – 06:00pm: Gilles Bareilles (Université Grenoble Alpes)
Thursday, October 13th, 2022 (Workshop only)
09:00am – 10:00am: Daniela Tonon (Università degli Studi di Padova)
10:00am – 10:30am: Coffee break
10:30am – 11:00am: François Delarue (Université Côte d'Azur)
11:00am – 11:30am: Aymeric Jacob de Cordemoy (Université de Pau)
11:30am – 12:00pm: Hippolyte Labarrière (INSA Toulouse)
12:00pm – 02:00pm: Lunch time
Buffet for workshop attendeees at Laboratoire J.A. Dieudonné
02:00pm – 03:00pm: Edouard Pauwels (Université Toulouse 3 Paul Sabatier)
03:00pm – 03:30pm: Stephen Becker (University of Colorado at Boulder)
03:30pm – 04:00pm: Coffee break
04:00pm – 04:30pm: Baptiste Plaquevent-Jourdain (Inria Paris & Université de Sherbrooke)
04:30pm – 05:00pm: Vo Anh Thuong Nguyen (Université de Perpignan)
07:30pm: Dinner at L'Union
Where: 1 Rue Michelet, 06100 Nice (Google Maps)
Friday, October 14th, 2022 (Workshop only)
09:00am – 10:00am: Yannick Privat (Université de Strasbourg)
10:00am – 10:30am: Coffee break
10:30am – 11:00am: Bernard Bonnard (Université de Bourgogne)
11:00am – 11:30am: Alesia Herasimenka (Université Côte d'Azur)
11:30am – 12:00pm: Jean-Jacques Godeme (Université de Normandie)
12:00pm – 12:30pm: Workshop closing & farewell
Abstracts
Gilles Bareilles (Université Grenoble Alpes)
Title: Méthodes de Newton pour l'optimisation composite non-lisse
Abstract: Beaucoup de problèmes d'optimisation de machine learning ou de traitement du signal peuvent s'écrire comme la minimisation d'une composition de fonctions, non différentiable. Cette non-différentiabilité est souvent structurée en une collection de variétés lisses où la fonction est lisse. Nous proposons une méthode permettant d'identifier le sous-espace d'un minimiseur et, suivant la philosophie SQP, en déduisons des algorithmes rapides.
Stephen Becker (University of Colorado at Boulder)
Title: High-probability Convergence Bounds for Non-convex Stochastic Gradient Descent, with applications to learning
Abstract: Stochastic gradient descent is one of the most common iterative algorithms used in machine learning. While being computationally cheap to implement, recent literature suggests it may have implicit regularization properties that prevent over-fitting. We analyze the properties of stochastic gradient descent from a theoretical standpoint to help bridge the gap between theoretical and empirical results. We specifically tackle the case of heavy-tailed noise, since recent results have shown empirically that noise due to mini-batch sampling can be non-Gaussian. Most theoretical results either assume convexity or only provide convergence results in mean, while we prove convergence bounds in high probability without assuming convexity. By high-probability, we mean that for a given failure rate delta, our iteration complexity bounds depend polynomially on log(1/delta) rather than on 1/delta. Assuming strong smoothness, we prove high probability convergence bounds in two settings:
- assuming the Polyak-Lojasiewicz inequality and norm sub-Gaussian gradient noise, and
- assuming norm sub-Weibull gradient noise.
In the first setting, in the setting of statistical learning, we combine our convergence bounds with existing generalization bounds based on algorithmic stability in order to bound the true risk and show that for a certain number of epochs, convergence and generalization balance in such a way that the true risk goes to the empirical minimum as the number of samples goes to infinity. In the second setting, as an intermediate step to proving convergence, we prove a probability result of independent interest. The probability result extends Freedman-type concentration beyond the sub-exponential threshold to heavier-tailed martingale difference sequences. Joint work with: Liam Madden, Emiliano Dall’Anese. https://arxiv.org/abs/2006.05610
Bernard Bonnard (Université de Bourgogne)
Title: Optimal Control of the Lotka-Volterra équations with applications
Abstract: Recent research activities to control the infection of the gut microbiota are based on the n-dimensional Lotka-Volterra model generalizing the prey predator model. The controls are of antibiotics or probiotics which are of permanent type or transplantations and bactericides which belong to the sampled-data control category. Optimal control problems aim to reduce the infection. We discuss the proprerties of the dynamics revisiting the original work of Lotka-Voltera and present complementary results in the frame of optimal control in the permanent and sampled-data control frame.
François Delarue (Université Côte d'Azur)
Title: Weak solutions to the master equation of potential mean field games
Abstract: The purpose of this work is to introduce a notion of weak solution to the master equation of a potential mean field game and to prove that existence and uniqueness hold under quite general assumptions. Remarkably, this is achieved without any monotonicity constraint on the coefficients.
Jean-Jacques Godeme (Université de Normandie)
Title: Provable Phase Retrieval via Mirror Descent
Abstract: In this paper, we consider the problem of phase retrieval, which consists of recovering an $n$-dimensional real vector from the magnitude of its \(m\) linear measurements. We propose a mirror descent (or Bregman gradient descent) algorithm based on a wisely chosen Bregman divergence, hence allowing to remove the classical global Lipschitz continuity requirement on the gradient of the nonconvex phase retrieval objective to be minimized. We apply the mirror descent for two random measurements: the i.i.d standard Gaussian and those obtained by multiple structured illuminations through Coded Diffraction Patterns (CDP). For the Gaussian case, we show that when the number of measurements m is large enough, then with high probability, for almost all initializers, the algorithm recovers the original vector up to a global sign change. For both measurements, the mirror descent exhibits a local linear convergence behaviour with a dimension-independent convergence rate. Our theoretical results are finally illustrated with various numerical experiments, including an application to the reconstruction of images in precision optics.
Sorin-Mihai Grad (ENSTA Paris)
Title: Relaxed-inertial proximal point algorithms for problems involving strongly quasiconvex functions
Abstract: Introduced in in the 1970's by Martinet for minimizing convex functions and extended shortly afterwards by Rockafellar towards monotone inclusion problems, the proximal point algorithm turned out to be a viable computational method for solving various classes of optimization problems, in particular with nonconvex objective functions. We propose first a relaxed-inertial proximal point type algorithm for solving optimization problems consisting in minimizing strongly quasiconvex functions whose variables lie in finitely dimensional linear subspaces. The method is then extended to equilibrium problems where the involved bifunction is strongly quasiconvex in the second variable. Possible modifications of the hypotheses that would allow the algorithms to solve similar problems involving quasiconvex functions are discussed, too. Numerical experiments confirming the theoretical results, in particular that the relaxed-inertial algorithms outperform their pure proximal point counterparts, are provided, too. This talk is based on joint work with Felipe Lara and Raúl Tintaya Marcavillaca (Universidad de Tarapacá).
Alesia Herasimenka (Université Côte d'Azur)
Title: Optimal Control of Solar Sails for a Sun Occultation Mission
Abstract: "Studying solar corona is fundamental to gain insight into a plethora of phenomena with major impact on satellite dynamics and operations. Due to the very-modest brightness of the corona (namely, roughly one million times weaker than the Sun), observations are achieved by means of coronagraphs, which are optical instruments provided with a mask to occult the Sun's disk. However, ground-based measurements suffer from scattering due to the atmosphere. A novel concept was recently proposed, which consists of using natural bodies as occulting disks [1] [2]. The idea is to place a satellite in proximity of the tip of the umbra cone generated by a celestial body (e.g., Earth or Moon). Assuming that electrical power is gathered via solar panels, the satellite is constrained to periodically leave the observation zone end expose itself to sunlight to recharge its batteries. The possibility of using a solar sail to maneuver the satellite in a propellantless fashion was suggested [2]. This work further investigates this option by offering a detailed study of optimal solar-sail-actuated maneuvers for repeated observations. The circular restricted three-body problem (Earth-Sun system, where Earth serves as occulting body) is used to model the motion of the satellite. Trajectory design is formulated as a periodic optimal control problem aimed at maximizing the duty cycle of the observations, defined as the fraction of orbital period devoted to observations. Charge of the batteries is part of the state variables, and its rate of change is function of the position of the satellite and increases from zero to its maximum value across the penumbra region. Pontryagin maximum principle (PMP) is then applied to deduce necessary conditions of optimality for the aforementioned cost function (duty cycle) and dynamical model. PMP reveals the periodicity of boundary conditions of both state and adjoint variables. Numerical solution is achieved by using indirect techniques. To this purpose, a reliable initial guess is obtained by outcomes of reference [1] and differential continuation is used to degrade the reflectivity of the sail and to explore various capacities of the batteries and size of the sail. Stability of the periodic trajectory is also discussed, as well as efficiency and convergence of the numerical methods. [1] Bernardini, Nicolo and Baresi, Nicola and Armellin, Roberto and Eckersley, Steve. (2020). Feasibility Study of Sun Occultation Missions Using Natural Bodies, International Astronautical Congress (IAC), IAF. [2] Eckersley, Steve and Kemble, Stephen (2017) Method of solar occultation, Google Patents, US Patent 9,676,50.
Aymeric Jacob de Cordemoy (Université de Pau)
Title: Problème d’optimisation de forme impliquant la loi de Tresca dans un cas scalaire
Abstract: Dans ce travail nous étudions, sans procédure de régularisation ou de pénalisation, un problème d’optimisation de forme impliquant un phénomène de frottement modélisé par la loi de Tresca dans un cas scalaire. Plus précisément, nous cherchons à calculer le gradient de forme de la fonctionnelle énergie qui va dépendre de la solution d'un problème de Tresca. Ce problème est non-linéaire et non lisse, par conséquent nous utilisons des outils d’analyse convexe tels que l’opérateur proximal ou encore la notion d’épi-différentiabilité d’ordre 2 , afin de prouver que la solution du problème de Tresca admet une dérivée directionnelle matérielle et de forme, et que celles-ci sont chacune l’unique solution d’un problème aux limites impliquant des conditions unilatérales de type Signorini. Enfin, à l’aide de ces dérivées directionnelles, nous caractérisons le gradient de forme de la fonctionnelle énergie, et nous exposons une direction de descente ce qui permettra de la minimiser numériquement.
Hippolyte Labarrière (INSA Toulouse)
Title: FISTA restart using an automatic estimation of the growth parameter
Abstract: We propose a restart scheme for FISTA (Fast Iterative Shrinking-Threshold Algorithm). This method which is a generalization of Nesterov's accelerated gradient algorithm is widely used in the field of large convex optimization problems and it provides fast convergence results under a strong convexity assumption. These convergence rates can be extended for weaker hypotheses such as the \L{}ojasiewicz property but it requires prior knowledge on the function of interest. In particular, most of the schemes providing a fast convergence for non-strongly convex functions satisfying a quadratic growth condition involve the growth parameter which is generally not known. Recent works show that restarting FISTA could ensure a fast convergence for this class of functions without requiring any knowledge on the growth parameter. We improve these restart schemes by providing a better asymptotical convergence rate and by requiring a lower computation cost. We present numerical results emphasizing the efficiency of this method.
Tam Le (Toulouse School of Economics)
Title: Subgradient sampling for Nonsmooth Nonconvex Minimization
Abstract: We consider a stochastic minimization problem in the nonsmooth and nonconvex setting which applies for instance to the training of deep learning models. A popular way in the machine learning community to deal with this problem is to use stochastic gradient descent (SGD). This method combines both subgradient sampling and backpropagation, which is an efficient implementation of the chain-rule formula on nonsmooth compositions. Due to the incompatibility of these operations in the nonsmooth world, the SGD can generates spurious critical points in the optimization landscape which does not guarantee the convergence of the objective function to a meaningful value. We will explain in this talk how the model of Conservative Gradients is compatible with subgradient sampling and backpropagation and allows to obtain convergence results for SGD. By means of definable geometry, we will emphasize that functions used in machine learning are locally endown with geometric properties of piecewise linear functions. In this setting, chain-ruling nonsmooth functions and sampling subgradients is fully justified, and spurious critical points are hardly attained when performing SGD in practice.
Vo Anh Thuong Nguyen (Université de Perpignan)
Title: Farthest distance function to strongly convex sets in Hilbert spaces
Abtract: The aim of this talk is twofold. On one hand, we show that the strong convexity of a set is equivalent to the semiconcavity of its associated farthest distance function. On the other hand, we establish that the farthest distance of a point to a strongly convex set is the minimum of farthest distances to the given point from suitable closed balls separating the set and the point.
Edouard Pauwels (Université Toulouse 3 Paul Sabatier)
Title: Nonsmooth differential calculus and optimization, the conservative gradient approach
Abstract: We are interested in the analysis of formal application of differential calculus rules to non-differentiable objects. This computationally efficient strategy had a world-wide empirical success, as it is and implemented in automatic differentiation routines in modern machine learning librairies, such as Tensorflow or Pytorch. First I will illustrate how blind application of compositional rules of differential calculus to nonsmooth objects can be problematic, requiring a proper mathematical model. Then I will introduce a weak notion of generalized derivative, named conservative gradients, and show its compatibility with compositional calculus, while maintaining optimization guaranties for first order methods of gradient type. The end of the talk will be dedicated to recent extension of conservative calculus beyond simple arithmetic operations.
Baptiste Plaquevent-Jourdain (Inria Paris & Université de Sherbrooke)
Title: On the B-differential of the componentwise minimum of two vectorial functions
Abstract: This work deals with the computation of the B-differential of the componentwise minimum of two functions \(F\) and \(G\) with values in \(R^n\). When these functions are affine, this problem, denote it \((i)\), has at least four other equivalent reformulations, which consist in $(ii)$~enumerating the sectors divided by an arrangement of hyperplanes containing the origin, $(iii)$~ascertaining the solvability of a homogeneous system of strict linear inequalities and every system with any number of inequalities reversed, $(iv)$~determining the orthants encountered by the null space of a matrix, and $(v)$~listing the linearly separable bipartitions of a finite set. Problem \((i)\) arises in the reformulation of the (linear) complementarity problem with the Min C-function, which was our initial motivation. The set to describe has a finite number of elements, which can be exponential. We propose an incremental algorithm to make this description, which is based on the formulations \((iii)\) and \((iv)\) and whose compatibility problems are expressed in terms of optimization problems, solved by an interior point technique. Thanks to this approach and to the exploitation of various properties of the B-differential, the total complexity of the algorithm is often much better in pratice than the ``brute force'' approach, without ever exceeding it. Numerical results are presented. Some aspects of the computation of the B-differential of two nonlinear functions ~\(F\) and ~\(G\) are also investigated, in particular, it is shown how the B-differential of the minimum of the linearized functions can ease its description."
Yannick Privat (Université de Strasbourg)
Title: Optimal location of resources for species survival
Abstract: In this work, we are interested in the analysis of optimal resources configurations (typically foodstuff) necessary for a species to survive. For that purpose, we use the logistic diffusive equation
\begin{equation}\tag{LDE}\label{LDE} \left\{ \begin{array}{ll} \partial_t\theta=\mu \Delta \theta(x)+(m(x)-\theta(x))\theta(x) & t>0, \ x\in \Omega,\\ \frac{\partial \theta}{\partial \nu} =0 &x\in \partial \Omega, \end{array} \right.\end{equation}where \(\theta\) is the population densities, \(m\) stands for the resources distribution and \(\mu>0\) stands for the species velocity also called diffusion rate. This system models the evolution of population density involving a term standing for the heterogeneous spreading (in space) of resources. The principal issue investigated in this talk writes: how to spread in an optimal way resources in a closed habitat? This problem can be recast
- either as the one of minimizing the principal eigenvalue of an elliptic operator,
- or maximizing the total population size (given by \(\int_\Omega \theta\))
with respect to the domain occupied by resources, under a volume constraint. By using symmetrization techniques, as well as necessary optimality conditions, we prove new qualitative results on the solutions. In particular, we investigate the optimality of particular configurations and the asymptotic behavior of optimizers as \(\mu\) tends to \(+\infty\).
Daniela Tonon (Università degli Studi di Padova)
Title: Hamilton-Jacobi equations on infinite dimensional spaces corresponding to linearly controlled gradient flows of an energy functional
Abstract: In this talk, we present a comparison principle for the Hamilton Jacobi (HJ) equation corresponding to linearly controlled gradient flows of an energy functional defined on a metric space. The main difficulties are given by the fact that the geometrical assumptions we require on the energy functional do not give any control on the growth of its gradient flow nor on its regularity. Therefore this framework is not covered by previous results on HJ equations on infinite dimensional spaces (whose study has been initiated in a series of papers by Crandall and Lions). Our proof of the comparison principle combines some rather classical ingredients, such as Ekeland’s perturbed optimization principle, with the use of the Tataru distance and of the regularizing properties of gradient flows in evolutional variational inequality formulation, that we exploit for constructing rigorous upper and lower bounds for the formal Hamiltonian. Our abstract results apply to a large class of examples, including gradient flows on Hilbert spaces and Wasserstein spaces equipped with a displacement convex energy functional satisfying McCann’s condition. Some hints on the existence of solutions will also be given.
Andrea Walther (HU Berlin)
Title: On Nonsmooth Optimization Based on Abs-Linearization
Abstract: For a so-called abs-smooth function, the concept of abs-linearization allows the generation of a piecewise linear local model that is provable of second order. Similar to the quadratic model generated by a truncated Taylor series in the smooth situation, this piecewise linear model can be used as a building block for optimization algorithms targeting nonsmooth problems of different kinds. In this talk, first we define abs-smooth functions covering a wide range of applications like clustering, image restoration, and robust gas network optimization. Also various mathematical models like complementarity problems or bilevel optimization tasks can be formulated as abs-smooth functions. Subsequently, the abs-linearization approach and the properties of the resulting local model will be illustrated. Then, we discuss the solution of piecewise linear optimization problems. Based on this capability we can derive optimization approaches that allow also the handling of constraints and/or nonlinearities. For each class of the nonsmooth optimization problems and the corresponding solution approach, convergence results and numerical examples will be given. Joint work with: Franz Bethke, Sabrina Fiege, Andreas Griewank, and Timo Kreimeier