One Piece of Math
This is a mirror of Samuel Vaiter's serie available on bluesky. All content is available under the CC BY-SA license.
Voronoi diagram and Delaunay tesselation
2025-04-07
A Voronoi diagram partitions space into regions closest to each point in a set. Its dual, the Delaunay triangulation, connects points to form triangles whose circumcircles contain no other points.
2025-04-07
A Voronoi diagram partitions space into regions closest to each point in a set. Its dual, the Delaunay triangulation, connects points to form triangles whose circumcircles contain no other points.
Low-Rank Adaptation (LoRA)
2025-03-28
LoRA (Low-Rank Adaptation) fine-tunes LLMs by updating low-rank matrices in attention layers while freezing most weights. It reduces memory and computational costs. [REF]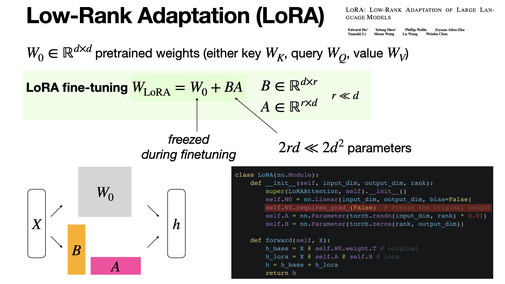
2025-03-28
LoRA (Low-Rank Adaptation) fine-tunes LLMs by updating low-rank matrices in attention layers while freezing most weights. It reduces memory and computational costs. [REF]

Graham’s scan
2025-03-27
Graham's Scan (1972) is an O(n log n) algorithm for finding the convex hull of a set of 2D points. It sorts points by polar angle, then builds the hull by pushing points onto a stack, popping them when a clockwise turn is detected. [REF]
2025-03-27
Graham's Scan (1972) is an O(n log n) algorithm for finding the convex hull of a set of 2D points. It sorts points by polar angle, then builds the hull by pushing points onto a stack, popping them when a clockwise turn is detected. [REF]
Hilbert's 17th problem
2025-03-26
Hilbert's 17th problem asks whether every multivariate polynomial that takes only non-negative values over the reals can be represented as a sum of squares of rational functions. Answered affirmatively by Artin in 1927. [REF]
2025-03-26
Hilbert's 17th problem asks whether every multivariate polynomial that takes only non-negative values over the reals can be represented as a sum of squares of rational functions. Answered affirmatively by Artin in 1927. [REF]

Moreau—Yosida regularization
2025-03-25
Moreau-Yosida regularization smooths a convex function by infimal convolution with a quadratic term, preserving convexity while gaining differentiability. [REF]
2025-03-25
Moreau-Yosida regularization smooths a convex function by infimal convolution with a quadratic term, preserving convexity while gaining differentiability. [REF]

Borwein integrals
2025-03-24
Borwein integrals are trigonometric integrals such that for odd n, they equal π/2 until the pattern breaks. [REF]
2025-03-24
Borwein integrals are trigonometric integrals such that for odd n, they equal π/2 until the pattern breaks. [REF]

Benamou—Brenier formulation of OT
2025-03-14
The Benamou-Brenier formulation of OT interprets Wasserstein distance as the minimal kinetic energy required to move one probability distribution into another over time. It links OT to mechanics via a dynamic viewpoint. [REF]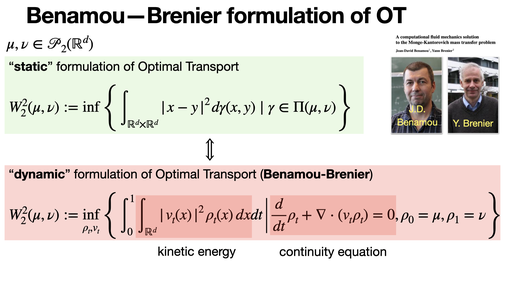
2025-03-14
The Benamou-Brenier formulation of OT interprets Wasserstein distance as the minimal kinetic energy required to move one probability distribution into another over time. It links OT to mechanics via a dynamic viewpoint. [REF]

Hermite-Hadamard inequality
2025-03-13
Hermite-Hadamard inequality bounds the average value of a convex function over an interval. It states that the function's value at the midpoint is less than or equal to the average value, which is, in turn, less than or equal to the average of the function's values at the endpoints.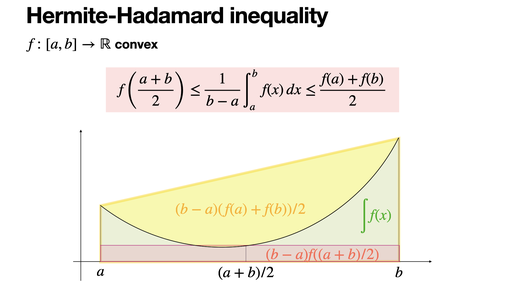
2025-03-13
Hermite-Hadamard inequality bounds the average value of a convex function over an interval. It states that the function's value at the midpoint is less than or equal to the average value, which is, in turn, less than or equal to the average of the function's values at the endpoints.

LayerNorm
2025-03-12
LayerNorm normalizes inputs by subtracting their mean and dividing by their standard deviation across features, looking like a projection onto a sphere for zero-mean data. A learnable affine transformation (scale and shift) adds flexibility. [REF]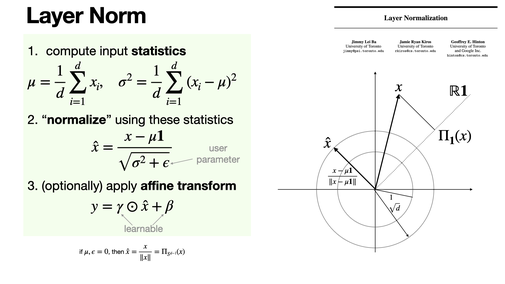
2025-03-12
LayerNorm normalizes inputs by subtracting their mean and dividing by their standard deviation across features, looking like a projection onto a sphere for zero-mean data. A learnable affine transformation (scale and shift) adds flexibility. [REF]

Quasiconvex function
2025-03-11
A quasiconvex function is one where all sublevel sets are convex, meaning for any u, { x | f(x) < u } is convex. Any local minima is a global one.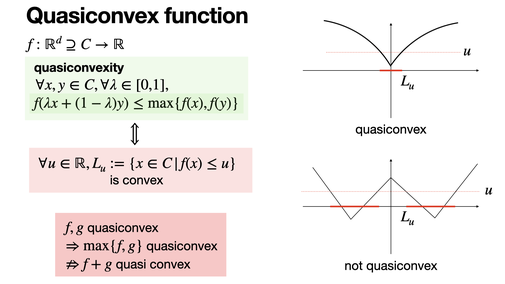
2025-03-11
A quasiconvex function is one where all sublevel sets are convex, meaning for any u, { x | f(x) < u } is convex. Any local minima is a global one.
Transformer
2025-03-10
Transformers revolutionized first NLP, then the whole ML world. It is built upon celebrated concepts like feedforward networks, normalization, residual connection, clever embeddings strategies, and the now essential (multi-head) attention mechanism. [REF]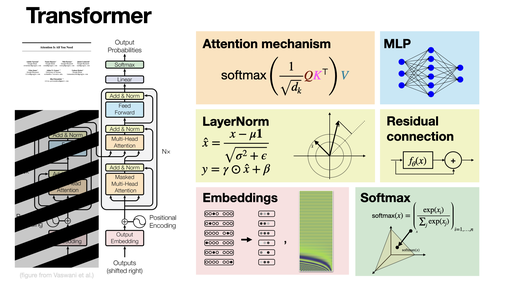
2025-03-10
Transformers revolutionized first NLP, then the whole ML world. It is built upon celebrated concepts like feedforward networks, normalization, residual connection, clever embeddings strategies, and the now essential (multi-head) attention mechanism. [REF]

(Homogeneous) Poisson process
2025-02-28
The Poisson process is a counting process that models the number of "rare" events occurring in a fixed interval of time or space. It has stationary and independent increments, and the time between events follows an exponential distribution.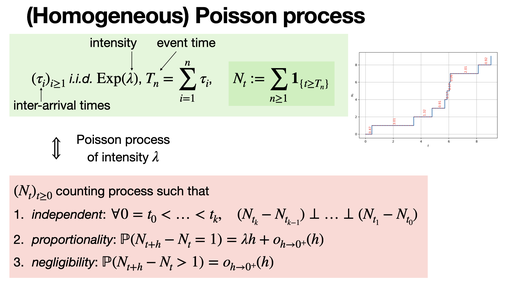
2025-02-28
The Poisson process is a counting process that models the number of "rare" events occurring in a fixed interval of time or space. It has stationary and independent increments, and the time between events follows an exponential distribution.

Brunn–Minkowski Theorem
2025-02-27
The Brunn–Minkowski theorem states that for nonempty compact set in Rn, the volume of their Minkowski sum is at least the sum of the nth roots of their volumes. It implies many inequalities in convex geometry including the isoperimetric inequality.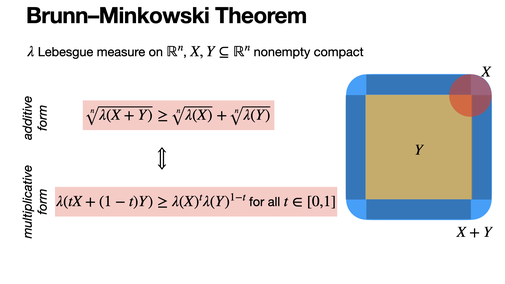
2025-02-27
The Brunn–Minkowski theorem states that for nonempty compact set in Rn, the volume of their Minkowski sum is at least the sum of the nth roots of their volumes. It implies many inequalities in convex geometry including the isoperimetric inequality.

Residual connection
2025-02-26
ResNet was a major milestone in deep learning by (re-)introducing skip connections, where networks try to learn residual mappings instead of identity. This allows very deep models, and is used in most modern architectures, including Transformers. [REF]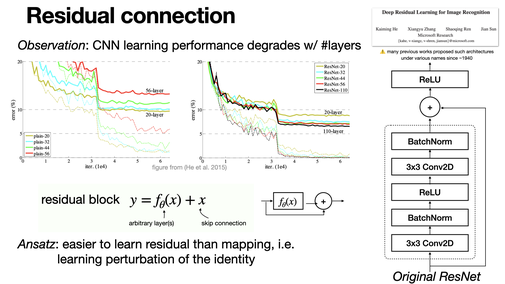
2025-02-26
ResNet was a major milestone in deep learning by (re-)introducing skip connections, where networks try to learn residual mappings instead of identity. This allows very deep models, and is used in most modern architectures, including Transformers. [REF]

Hausdorff distance
2025-02-25
The Hausdorff distance quantifies how far two sets are from each other by measuring the largest minimal distance needed to cover one with the other. It captures worst-case deviation: if one set has points far from the other, the distance is large.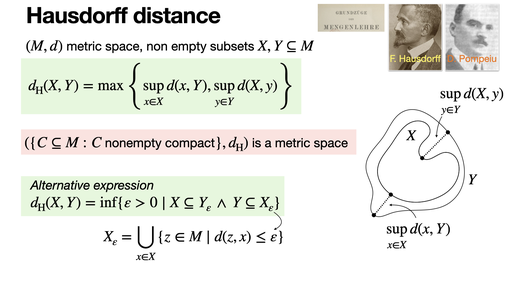
2025-02-25
The Hausdorff distance quantifies how far two sets are from each other by measuring the largest minimal distance needed to cover one with the other. It captures worst-case deviation: if one set has points far from the other, the distance is large.

Signed distance function (SDF)
2025-02-24
Signed Distance Functions/Fields define shapes implicitly by measuring the shortest distance from any point to the surface. Negative values are inside, and positive values are outside. SDFs allow smooth blending, Boolean operations for procedural modeling. [REF]
2025-02-24
Signed Distance Functions/Fields define shapes implicitly by measuring the shortest distance from any point to the surface. Negative values are inside, and positive values are outside. SDFs allow smooth blending, Boolean operations for procedural modeling. [REF]
McKean—Vlasov process
2025-02-07
The McKean-Vlasov equation drives stochastic processes where the drift and diffusion depend on both the state and the law of the process. It can be seen as the limit of interacting particle system, connecting stochastic dynamics with nonlinear Fokker-Planck equations. [REF]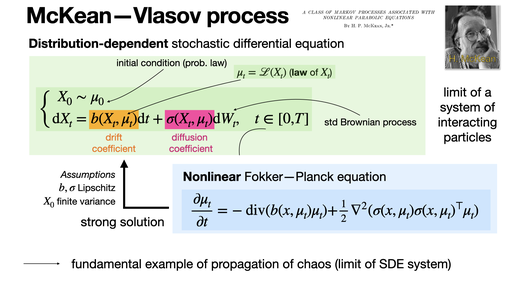
2025-02-07
The McKean-Vlasov equation drives stochastic processes where the drift and diffusion depend on both the state and the law of the process. It can be seen as the limit of interacting particle system, connecting stochastic dynamics with nonlinear Fokker-Planck equations. [REF]

From tokens to embeddings
2025-02-06
To get token embeddings, text is tokenized into tokens (e.g., via BPE). Each token is assigned a unique ID. IDs are converted to one-hot vectors, then multiplied by an embedding matrix (learned during training) to produce dense, fixed-size token embeddings.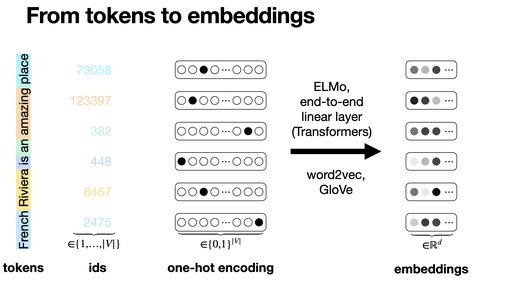
2025-02-06
To get token embeddings, text is tokenized into tokens (e.g., via BPE). Each token is assigned a unique ID. IDs are converted to one-hot vectors, then multiplied by an embedding matrix (learned during training) to produce dense, fixed-size token embeddings.

Mathematical morphology
2025-02-05
Mathematical morphology studies shapes and structures in images using tools like erosion, dilation, opening, and closing. It was introduced by Matheron & Serra in the 60s. It is typically defined on abstract lattices. [REF]
2025-02-05
Mathematical morphology studies shapes and structures in images using tools like erosion, dilation, opening, and closing. It was introduced by Matheron & Serra in the 60s. It is typically defined on abstract lattices. [REF]
Rudin—Osher—Fatemi denoising
2025-02-04
The Rudin-Osher-Fatemi (ROF) model is a method in image denoising. It minimizes the total variation of an image (preserving edges) while trying to be close in the L2 sense to the observations. [REF]
2025-02-04
The Rudin-Osher-Fatemi (ROF) model is a method in image denoising. It minimizes the total variation of an image (preserving edges) while trying to be close in the L2 sense to the observations. [REF]
Tasks in Natural Language Processing
2025-02-03
Natural Language Processing is a broad field with several applications: next-token prediction, fill-in-the-middle, sentiment analysis, question answering, speech recognition (and text-to-speech), translation, etc. [REF]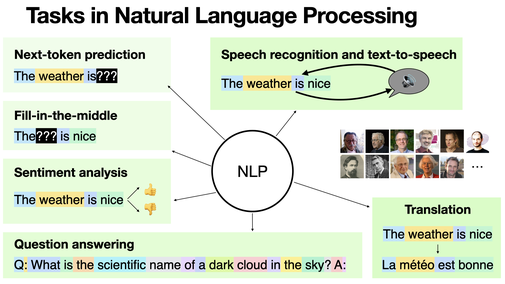
2025-02-03
Natural Language Processing is a broad field with several applications: next-token prediction, fill-in-the-middle, sentiment analysis, question answering, speech recognition (and text-to-speech), translation, etc. [REF]

Breadth-First Search vs Depth-First Search
2025-01-31
Breadth-First Search (BFS) explores all nodes level by level, using a queue. Depth-First Search (DFS) goes deep into one branch before backtracking, using a stack/recursion.
2025-01-31
Breadth-First Search (BFS) explores all nodes level by level, using a queue. Depth-First Search (DFS) goes deep into one branch before backtracking, using a stack/recursion.
Byte Pair Encoding (BPE)
2025-01-30
Byte Pair Encoding is a tokenization method that starts with all characters as initial tokens. It iteratively merges the most frequent adjacent byte pairs in the text, adding new tokens to the vocabulary until reaching a predefined size. The output is a sequence of subword tokens. [REF]
2025-01-30
Byte Pair Encoding is a tokenization method that starts with all characters as initial tokens. It iteratively merges the most frequent adjacent byte pairs in the text, adding new tokens to the vocabulary until reaching a predefined size. The output is a sequence of subword tokens. [REF]
Cyclic projection onto convex sets
2025-01-29
Cyclic projection onto convex sets is a method to find a point in the intersection of convex sets. It iteratively projects onto each set in a cycle, and it converges to a point in the intersection under restrictive assumptions. [REF]
2025-01-29
Cyclic projection onto convex sets is a method to find a point in the intersection of convex sets. It iteratively projects onto each set in a cycle, and it converges to a point in the intersection under restrictive assumptions. [REF]
(Unmasked) Attention
2025-01-28
A single-head attention layer processes a sequence by assigning relevance scores between elements. It computes these scores to decide how much focus each part of the seq should receive and combines the information. [REF]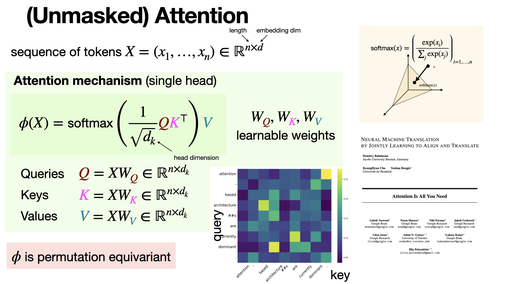
2025-01-28
A single-head attention layer processes a sequence by assigning relevance scores between elements. It computes these scores to decide how much focus each part of the seq should receive and combines the information. [REF]

Zeros of random (normal) polynomial
2025-01-27
Zeros of random polynomials with i.i.d. coefficients exhibit interesting convergence properties. In particular, normal coefficient leads to weak convergence of the empirical measure to the unit circle. [REF]
2025-01-27
Zeros of random polynomials with i.i.d. coefficients exhibit interesting convergence properties. In particular, normal coefficient leads to weak convergence of the empirical measure to the unit circle. [REF]
Neural Language Model
2025-01-24
The Neural Probabilistic Language Model (Bengio et al., 2000) introduced joint use of word embeddings and neural networks for next-token prediction. It replaced n-gram models by mapping words to a continuous vector space, and the use a standard neural networks architectures. [REF]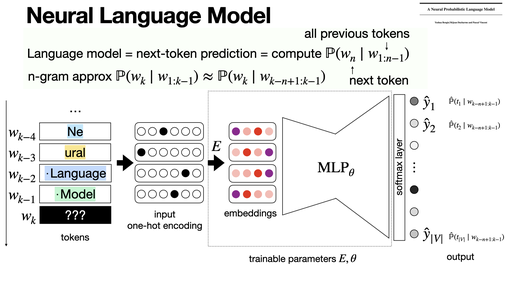
2025-01-24
The Neural Probabilistic Language Model (Bengio et al., 2000) introduced joint use of word embeddings and neural networks for next-token prediction. It replaced n-gram models by mapping words to a continuous vector space, and the use a standard neural networks architectures. [REF]

Neural ODE and ResNet
2025-01-23
ResNet and Neural ODEs are closely related: ResNet uses discrete residual/skip connections, while Neural ODEs generalize this to continuous transformations using ODEs. Neural ODEs can be seen as the limit of ResNet as the number of layers approaches infinity. [REF]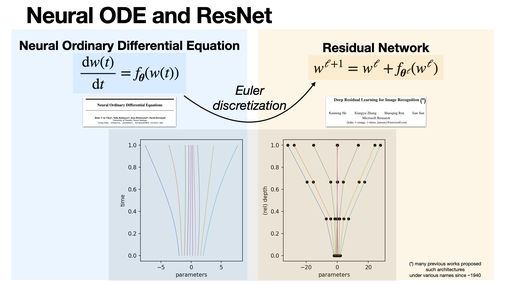
2025-01-23
ResNet and Neural ODEs are closely related: ResNet uses discrete residual/skip connections, while Neural ODEs generalize this to continuous transformations using ODEs. Neural ODEs can be seen as the limit of ResNet as the number of layers approaches infinity. [REF]

Marchenko–Pastur law
2025-01-22
The Marchenko–Pastur law describes the limiting spectral distribution of eigenvalues of large random covariance matrices. The theorem proves that as dimensions grow, the empirical spectral distribution converges weakly to this law. [REF]
2025-01-22
The Marchenko–Pastur law describes the limiting spectral distribution of eigenvalues of large random covariance matrices. The theorem proves that as dimensions grow, the empirical spectral distribution converges weakly to this law. [REF]
Singular Value Decomposition (SVD)
2025-01-21
Singular Value Decomposition is a matrix factorization that expresses a matrix M as UΣVᵀ, where U and V are orthogonal matrices, and Σ is diagonal. It can interpreted as the action of a rotation, a scaling and a rotation/reflection. [REF]
2025-01-21
Singular Value Decomposition is a matrix factorization that expresses a matrix M as UΣVᵀ, where U and V are orthogonal matrices, and Σ is diagonal. It can interpreted as the action of a rotation, a scaling and a rotation/reflection. [REF]
Napoleon's problem
2025-01-20
Napoleon's problem asks to construct the center of a circle with only a compass. It is possible to solve it with six circles. [REF]
2025-01-20
Napoleon's problem asks to construct the center of a circle with only a compass. It is possible to solve it with six circles. [REF]
Soft(arg)max
2025-01-17
Soft(arg)max function transforms logits into probability vector. One shows that softmax (w/ temperature) converges pointwise to the argmax, selecting the most likely outcome. Essential in in multinomial logistic regression and for attention mechanisms
2025-01-17
Soft(arg)max function transforms logits into probability vector. One shows that softmax (w/ temperature) converges pointwise to the argmax, selecting the most likely outcome. Essential in in multinomial logistic regression and for attention mechanisms
Cheap gradient principle
2025-01-16
The Cheap Gradient Principle (Baur—Strassen, 1983) states that computing gradients via automatic differentiation is efficient: the gradient of a function f can be obtained with a cost proportional to evaluating f
2025-01-16
The Cheap Gradient Principle (Baur—Strassen, 1983) states that computing gradients via automatic differentiation is efficient: the gradient of a function f can be obtained with a cost proportional to evaluating f

Group
2025-01-15
A group is one of the most fundamental structure in algebra: a set paired with a binary operation satisfying associativity, identity, and invertibility. Exemples include the real line, integers with addition, modular addition, symmetric group, rotations, etc.
2025-01-15
A group is one of the most fundamental structure in algebra: a set paired with a binary operation satisfying associativity, identity, and invertibility. Exemples include the real line, integers with addition, modular addition, symmetric group, rotations, etc.

Topological order
2025-01-14
Topological order is a total (all elements are comparable) order of vertices in a directed acyclic graph where for every directed edge u→v, vertex u appears before v in the order. It’s used in tasks like scheduling, circuit design and automatic differentiation.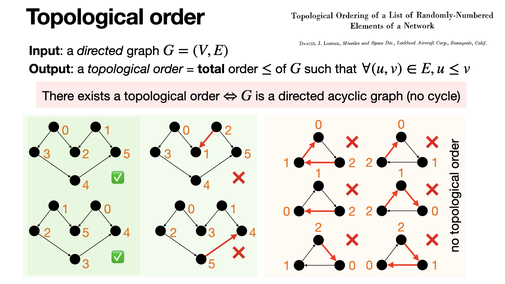
2025-01-14
Topological order is a total (all elements are comparable) order of vertices in a directed acyclic graph where for every directed edge u→v, vertex u appears before v in the order. It’s used in tasks like scheduling, circuit design and automatic differentiation.

A one line proof of Sum of Two Squares Thm
2025-01-13
Heath-Brown/Zagier proofs of Fermat’s sum of two squares theorem relies on the fact that the cardinalities of a set and the fixed points of an involution on it have the same parity. [REF]
2025-01-13
Heath-Brown/Zagier proofs of Fermat’s sum of two squares theorem relies on the fact that the cardinalities of a set and the fixed points of an involution on it have the same parity. [REF]

Typical complexities when analyzing algorithms
2025-01-10
Algorithm (asymptotic) complexity typically measures time or space required as input size grows. They are measured against a model of computation, typically a Turing machine or variations.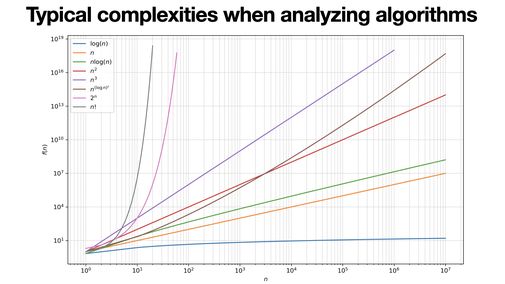
2025-01-10
Algorithm (asymptotic) complexity typically measures time or space required as input size grows. They are measured against a model of computation, typically a Turing machine or variations.

Tropical geometry
2025-01-09
Tropical geometry studies algebraic varieties through the "tropical semiring" where addition is min (or max) and multiplication is the regular addition. It transforms polynomial eqs into piecewise linear structures and is linked to dynamic programming. [REF]
2025-01-09
Tropical geometry studies algebraic varieties through the "tropical semiring" where addition is min (or max) and multiplication is the regular addition. It transforms polynomial eqs into piecewise linear structures and is linked to dynamic programming. [REF]

Brownian motion
2025-01-08
Brownian motion is the fundamental martingale that arises in almost all areas of mathematics with a stochastic aspect, used in biology, passing by statistical mechanics and diffusion model. [REF]
2025-01-08
Brownian motion is the fundamental martingale that arises in almost all areas of mathematics with a stochastic aspect, used in biology, passing by statistical mechanics and diffusion model. [REF]
Nadaraya—Watson kernel estimator
2025-01-07
The Nadaraya-Watson estimator is linear local averaging estimator relying on a pointwise nonnegative kernel. Most of the time, a box or Gaussian kernel is used. [REF]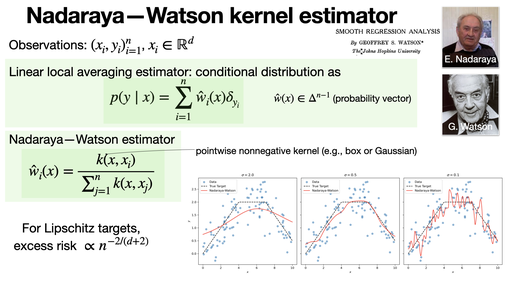
2025-01-07
The Nadaraya-Watson estimator is linear local averaging estimator relying on a pointwise nonnegative kernel. Most of the time, a box or Gaussian kernel is used. [REF]

Partly smooth function (in the convex case)
2025-01-06
The concept of partly smooth functions (Lewis '02) unifies many nonsmooth functions, capturing their geometry: smooth along the manifold and sharp normal to it. It allows fine sensitivity analysis results. In the convex case, it generalizes sparsity.
2025-01-06
The concept of partly smooth functions (Lewis '02) unifies many nonsmooth functions, capturing their geometry: smooth along the manifold and sharp normal to it. It allows fine sensitivity analysis results. In the convex case, it generalizes sparsity.

Inversion in the complex plane
2025-01-03
Complex transformation lead to fun visual effects. Inversion is a transformation that maps a point to its reflection through a circle. It is conformal, meaning it preserves angles. [REF]
2025-01-03
Complex transformation lead to fun visual effects. Inversion is a transformation that maps a point to its reflection through a circle. It is conformal, meaning it preserves angles. [REF]
Basic Game of Life demo
2025-01-02
The Game of Life is a cellular automaton devised by John Conway in 1970. It consists of a grid of cells that evolve according to simple deterministic rules. Despite the simplicity of the rules, the Game of Life can exhibit complex behavior. [REF]
2025-01-02
The Game of Life is a cellular automaton devised by John Conway in 1970. It consists of a grid of cells that evolve according to simple deterministic rules. Despite the simplicity of the rules, the Game of Life can exhibit complex behavior. [REF]
Smoothstep functions
2025-01-01
Smoothstep functions are a family of functions that interpolate between 0 and 1 smoothly. They are used in computer graphics to create smooth transitions between colors or shapes. [REF]
2025-01-01
Smoothstep functions are a family of functions that interpolate between 0 and 1 smoothly. They are used in computer graphics to create smooth transitions between colors or shapes. [REF]
Mandelbrot zoom
2024-12-31
The Mandelbrot set is a fractal defined by iterating the complex map z² + c. Zooming in reveals patterns and self-similarity at all scales. [REF]
2024-12-31
The Mandelbrot set is a fractal defined by iterating the complex map z² + c. Zooming in reveals patterns and self-similarity at all scales. [REF]
Sierpinski triangle
2024-12-30
The Sierpinski triangle is a fractal with the property of self-similarity. It is constructed by iteratively removing the central triangle of each triangle in a sequence of triangles. [REF]
2024-12-30
The Sierpinski triangle is a fractal with the property of self-similarity. It is constructed by iteratively removing the central triangle of each triangle in a sequence of triangles. [REF]
Cyclide
2024-12-27
A cyclide is a surface that is a generalization of the torus and can be defined as the envelope of a family of spheres.
2024-12-27
A cyclide is a surface that is a generalization of the torus and can be defined as the envelope of a family of spheres.
Whitney umbrella
2024-12-26
The equation x² − y²z = 0 describes the Whitney umbrella. It is a ruled surface with a cusp at the origin.
2024-12-26
The equation x² − y²z = 0 describes the Whitney umbrella. It is a ruled surface with a cusp at the origin.
Fermat’s Christmas theorem
2024-12-25
Fermat's theorem on sums of two squares is a result of number theory that was first described in a letter of Fermat to Mersenne on December 25, 1640. It was first proved a century later by Euler in 1749. [REF]
2024-12-25
Fermat's theorem on sums of two squares is a result of number theory that was first described in a letter of Fermat to Mersenne on December 25, 1640. It was first proved a century later by Euler in 1749. [REF]

Moebius strip
2024-12-24
The Möbius strip is a one-sided surface with no boundaries, formed by twisting a strip of paper 180° and joining its ends.
2024-12-24
The Möbius strip is a one-sided surface with no boundaries, formed by twisting a strip of paper 180° and joining its ends.
Cayley singular cubic
2024-12-23
The algebraic surface (x+y+z)² + xyz = 0 is one of Cayley singular cubic. Cayley classifies them in 23 cases. [REF]
2024-12-23
The algebraic surface (x+y+z)² + xyz = 0 is one of Cayley singular cubic. Cayley classifies them in 23 cases. [REF]
Spirograph
2024-12-20
A spirograph is a parametric curve generated by tracing a point fixed on a circle as it rolls along the inside or outside of another circle. The resulting pattern depends on the radius of the circles and the point's position. [REF]
2024-12-20
A spirograph is a parametric curve generated by tracing a point fixed on a circle as it rolls along the inside or outside of another circle. The resulting pattern depends on the radius of the circles and the point's position. [REF]
Implicit bias of gradient descent on OLS
2024-12-19
When optimization problems have multiple minima, algorithms favor specific solutions due to their implicit bias. For ordinary least squares (OLS), gradient descent inherently converges to the minimal norm solution among all possible solutions. [REF]
2024-12-19
When optimization problems have multiple minima, algorithms favor specific solutions due to their implicit bias. For ordinary least squares (OLS), gradient descent inherently converges to the minimal norm solution among all possible solutions. [REF]
Linearly inducible orderings
2024-12-18
Linearly inducible orderings of n points in d-dimensional space are determined by projections onto a reference vector. Their combinatorial are typically less than the number of permutations n! (except when d ≥ n-1). [REF]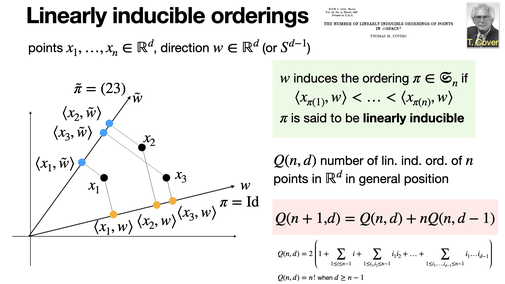
2024-12-18
Linearly inducible orderings of n points in d-dimensional space are determined by projections onto a reference vector. Their combinatorial are typically less than the number of permutations n! (except when d ≥ n-1). [REF]

An increasing continuous singular function
2024-12-17
There exists f:[0,1]→[0,1] strictly increasing, continuous function such that its derivative is 0 almost everywhere. [REF]
2024-12-17
There exists f:[0,1]→[0,1] strictly increasing, continuous function such that its derivative is 0 almost everywhere. [REF]

Gauss—Lucas theorem
2024-12-16
Gauss-Lucas theorem states that the roots of the derivative of a polynomial with complex coefficients always lie within the convex hull of the original polynomial's roots.
2024-12-16
Gauss-Lucas theorem states that the roots of the derivative of a polynomial with complex coefficients always lie within the convex hull of the original polynomial's roots.
Automatic differentiation: forward mode
2024-12-13
Automatic differentiation in forward mode computes derivatives by breaking down functions into elem operations and propagating derivatives alongside values. It’s efficient for functions with fewer inputs than outputs and for Jacobian-vect prod, using for instance dual numbers.
2024-12-13
Automatic differentiation in forward mode computes derivatives by breaking down functions into elem operations and propagating derivatives alongside values. It’s efficient for functions with fewer inputs than outputs and for Jacobian-vect prod, using for instance dual numbers.
Sinkhorn—Knopp algorithm
2024-12-12
The Sinkhorn—Knopp algorithm is an iterative method for approximating entropic optimal transport solutions. It balances two dual vectors through iterative rescaling leading to a matrix that respects marginals. Thanks to its parallel nature, it’s easy to implement on GPU for ML.
2024-12-12
The Sinkhorn—Knopp algorithm is an iterative method for approximating entropic optimal transport solutions. It balances two dual vectors through iterative rescaling leading to a matrix that respects marginals. Thanks to its parallel nature, it’s easy to implement on GPU for ML.
Perlin's noise
2024-12-11
Perlin’s noise generates smooth textures by assigning random gradient vectors to grid points and blending values through smooth interpolation. It is used in graphics, terrain, and textures generation. [REF]
2024-12-11
Perlin’s noise generates smooth textures by assigning random gradient vectors to grid points and blending values through smooth interpolation. It is used in graphics, terrain, and textures generation. [REF]
Newton's method for root finding
2024-12-10
Newton's method is an iterative root-finding algorithm that uses the derivative of a function to approximate a root. It converges quadratically, but may fail to converge or converge to a wrong root if the initial guess is not close enough.
2024-12-10
Newton's method is an iterative root-finding algorithm that uses the derivative of a function to approximate a root. It converges quadratically, but may fail to converge or converge to a wrong root if the initial guess is not close enough.
Kuratowski's theorem
2024-12-09
Kuratowski's theorem states that a graph is planar (can be drawn on a plane without edge crossings) iff it does not contain a subgraph that is a subdivision of either K₅ or K₃,₃. [REF]
2024-12-09
Kuratowski's theorem states that a graph is planar (can be drawn on a plane without edge crossings) iff it does not contain a subgraph that is a subdivision of either K₅ or K₃,₃. [REF]

Zonotopes and Zonoids
2024-12-06
A zonoid is a convex body that is a limit of zonotope (polytopes formed by the Minkowski sum of line segments). Bourgain et al. gave a precise number of segments required to approximate a zonoid by a zonotope in Hausdorff metric for a precision. [REF]
2024-12-06
A zonoid is a convex body that is a limit of zonotope (polytopes formed by the Minkowski sum of line segments). Bourgain et al. gave a precise number of segments required to approximate a zonoid by a zonotope in Hausdorff metric for a precision. [REF]
Morley's theorem
2024-12-05
Morley's theorem (1899) states that the intersections of the adjacent angle trisectors of any triangle defines an equilateral triangle. [REF]
2024-12-05
Morley's theorem (1899) states that the intersections of the adjacent angle trisectors of any triangle defines an equilateral triangle. [REF]
A one line proof of Cauchy—Schwarz
2024-12-04
Classical trinom proof of Cauchy-Schwarz is boring! It can be proved using only the squared norm of the addition. [REF]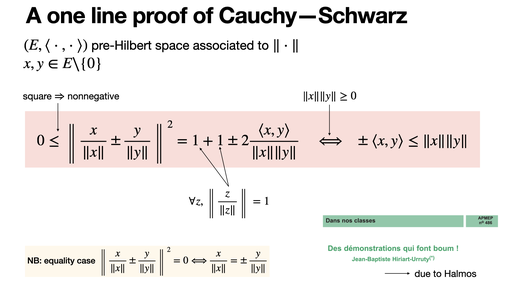
2024-12-04
Classical trinom proof of Cauchy-Schwarz is boring! It can be proved using only the squared norm of the addition. [REF]

Some image datasets in supervised learning
2024-12-03
There are a lot of different datasets in computer vision, with various dimensions, number of classes, text annotations or different kind of structural information (e.g., bounding boxes). Some popular general datasets are MNIST, CIFAR10/100, Pascal VOC, ImageNet and COCO.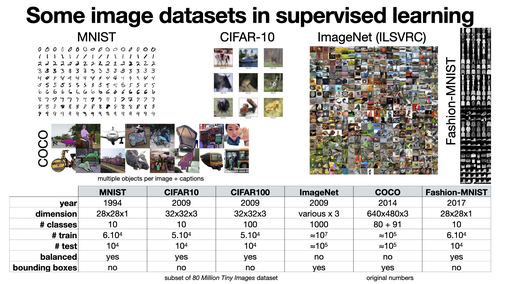
2024-12-03
There are a lot of different datasets in computer vision, with various dimensions, number of classes, text annotations or different kind of structural information (e.g., bounding boxes). Some popular general datasets are MNIST, CIFAR10/100, Pascal VOC, ImageNet and COCO.

Birkhoff contraction theorem
2024-12-02
Birkhoff's contraction theorem states that linear nonnegative (i.e. such that the image of the cone is contained in itself) mappings are contraction with respect to the Hilbert metric. In particular, it allows to use Banach fixed point theorem .[REF]
2024-12-02
Birkhoff's contraction theorem states that linear nonnegative (i.e. such that the image of the cone is contained in itself) mappings are contraction with respect to the Hilbert metric. In particular, it allows to use Banach fixed point theorem .[REF]

Bigram model
2024-11-29
A bigram model is a language model that predicts the next token based only on the previous one. It is an example of a discrete Markov chain, and was in fact one of the first motivation of Markov himself. [REF]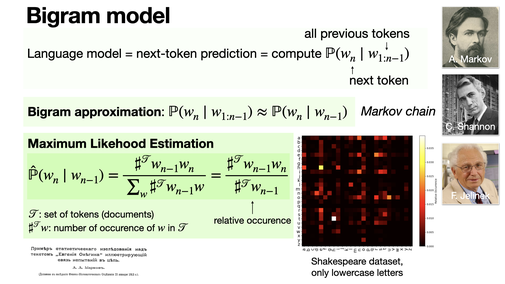
2024-11-29
A bigram model is a language model that predicts the next token based only on the previous one. It is an example of a discrete Markov chain, and was in fact one of the first motivation of Markov himself. [REF]

Two Fenchel dual problems
2024-11-28
When trying to compute a dual of a composite problem involving two functions and two linear operators (e.g., Total Variation regularization of inverse problems), it is sometimes useful to consider either of the operators as the dual operator.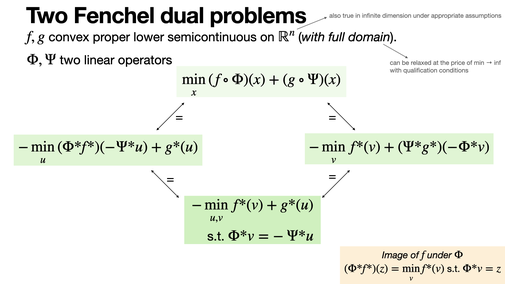
2024-11-28
When trying to compute a dual of a composite problem involving two functions and two linear operators (e.g., Total Variation regularization of inverse problems), it is sometimes useful to consider either of the operators as the dual operator.

Shannon’s entropy
2024-11-27
Shannon's entropy measures the uncertainty or information content in a probability distribution. It's an important concept in data compression and communication introduced in the seminal paper “A Mathematical Theory of Communication”. [REF]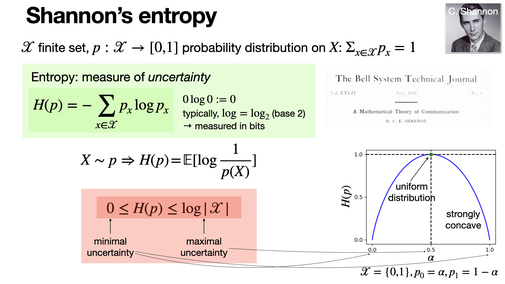
2024-11-27
Shannon's entropy measures the uncertainty or information content in a probability distribution. It's an important concept in data compression and communication introduced in the seminal paper “A Mathematical Theory of Communication”. [REF]

Banach—Steinhaus theorem
2024-11-26
The Banach-Steinhaus theorem, or Uniform Boundedness Principle, is a key result in functional analysis. It states that for a family of continuous linear operators on a Banach space, pointwise boundedness implies uniform boundedness. [REF]
2024-11-26
The Banach-Steinhaus theorem, or Uniform Boundedness Principle, is a key result in functional analysis. It states that for a family of continuous linear operators on a Banach space, pointwise boundedness implies uniform boundedness. [REF]

Hilbert metric
2024-11-25
The Hilbert projective (constant on rays) metric is a way to measure distances within a convex cone in a vector space. It is an important tool in hyperbolic geometry and for Perron-Frobenius theory. [REF]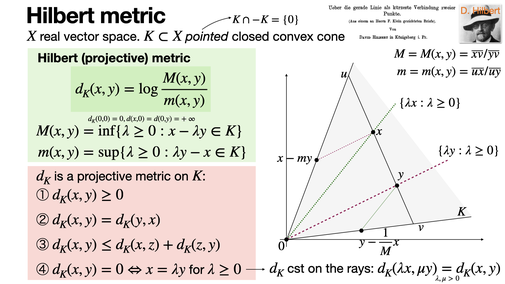
2024-11-25
The Hilbert projective (constant on rays) metric is a way to measure distances within a convex cone in a vector space. It is an important tool in hyperbolic geometry and for Perron-Frobenius theory. [REF]

Mersenne primes & Lucas—Lehmer test
2024-11-22
Mersenne primes are of the form Mₙ = 2ⁿ - 1, where n itself is a prime number. The Lucas-Lehmer test is an efficient method to check if Mₙ is prime. It iterates a sequence mod Mₙ to determine primality as used by the GIMPS project. [REF]
2024-11-22
Mersenne primes are of the form Mₙ = 2ⁿ - 1, where n itself is a prime number. The Lucas-Lehmer test is an efficient method to check if Mₙ is prime. It iterates a sequence mod Mₙ to determine primality as used by the GIMPS project. [REF]

Bubble sort
2024-11-21
Bubble Sort is an adaptative sorting algorithm that compares adjacent items, and swaps them if they're in the wrong order. It is easy to understand and implement, but inefficient in both the worst and average cases. [REF]
2024-11-21
Bubble Sort is an adaptative sorting algorithm that compares adjacent items, and swaps them if they're in the wrong order. It is easy to understand and implement, but inefficient in both the worst and average cases. [REF]
Tokenizer
2024-11-20
Tokenization is the process of breaking text into smaller units - tokens - which can be words, subwords, or characters. It's a step in NLP, transforming raw text into token embeddings. The classical algorithm is Byte-Pair Encoding at the subword level. [REF]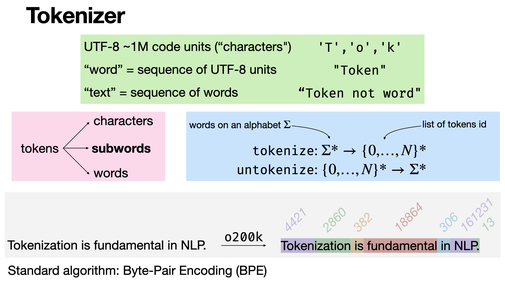
2024-11-20
Tokenization is the process of breaking text into smaller units - tokens - which can be words, subwords, or characters. It's a step in NLP, transforming raw text into token embeddings. The classical algorithm is Byte-Pair Encoding at the subword level. [REF]

Lorenz attractor
2024-11-19
The Lorenz system is a model that describes chaotic behavior in atmospheric convection. Its study reveals how small changes in initial conditions can lead to different outcomes. [REF]
2024-11-19
The Lorenz system is a model that describes chaotic behavior in atmospheric convection. Its study reveals how small changes in initial conditions can lead to different outcomes. [REF]
Nets, Covering & Packing Numbers
2024-11-18
Covering numbers can be thought as way to quantify “compactness” of a set in a complete metric space. It is also closely related to packing numbers. [REF]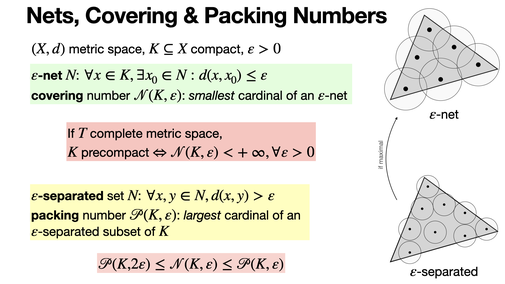
2024-11-18
Covering numbers can be thought as way to quantify “compactness” of a set in a complete metric space. It is also closely related to packing numbers. [REF]

(Girard)-Hutchinson estimator
2024-11-15
Hutchinson's estimator is a stochastic method for approximating the trace of large square matrices. It requires only matrix-vector products, allowing to compute the trace of implicitly defined matrices. It is useful in several settings (cross-validation, trace of the Hessian, etc). [REF]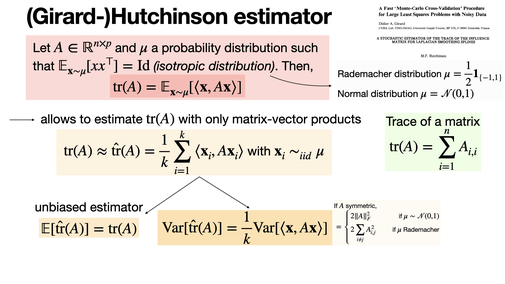
2024-11-15
Hutchinson's estimator is a stochastic method for approximating the trace of large square matrices. It requires only matrix-vector products, allowing to compute the trace of implicitly defined matrices. It is useful in several settings (cross-validation, trace of the Hessian, etc). [REF]

Graph Isomorphism
2024-11-14
Graph isomorphism problem asks the following question: given two finite graphs, are they isomorphic? There is no definite answer if it is in P, NP-complete or in another class (for the moment, it defines its proper complexity class GI). [REF] (in french)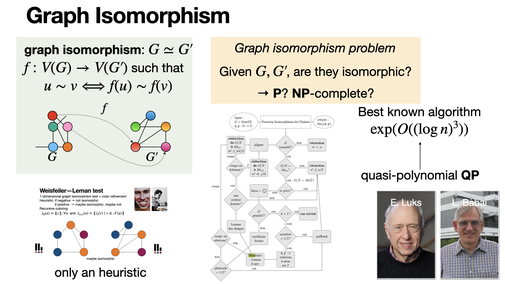
2024-11-14
Graph isomorphism problem asks the following question: given two finite graphs, are they isomorphic? There is no definite answer if it is in P, NP-complete or in another class (for the moment, it defines its proper complexity class GI). [REF] (in french)

Cumulative and quantile functions
2024-11-13
The cumulative distribution function (CDF) gives the probability that a random variable is less than or equal to a value. It characterizes a distribution. The quantile function (generalized inverse of the CDF) returns the value for a given cumulative probability.
2024-11-13
The cumulative distribution function (CDF) gives the probability that a random variable is less than or equal to a value. It characterizes a distribution. The quantile function (generalized inverse of the CDF) returns the value for a given cumulative probability.
Universal Approximation Theorem
2024-11-12
The Universal Approximation Theorem states that a feedforward neural network with a single hidden layer, using a non-linear activation function, can approximate any continuous function on a compact, given enough neurons. [REF]
2024-11-12
The Universal Approximation Theorem states that a feedforward neural network with a single hidden layer, using a non-linear activation function, can approximate any continuous function on a compact, given enough neurons. [REF]
Prim’s algorithm
2024-11-11
Prim's algorithm is a greedy method for finding the minimum spanning tree of a weighted, connected graph. It starts with any node and repeatedly adds the smallest edge that connects a visited node to an unvisited node. [REF]
2024-11-11
Prim's algorithm is a greedy method for finding the minimum spanning tree of a weighted, connected graph. It starts with any node and repeatedly adds the smallest edge that connects a visited node to an unvisited node. [REF]
What implies what? Probability version
2024-11-08
Convergence of random variables (and associated probability measures) comes in several modes: almost sure, Lp, in probability, but also in Wasserstein distance or Total Variation in the space of measures. [REF]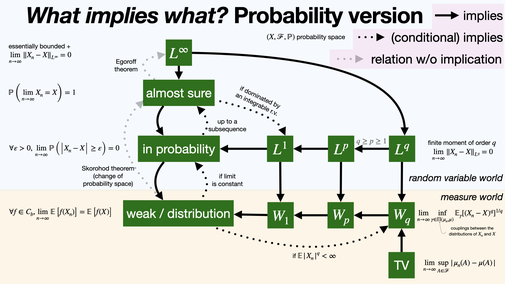
2024-11-08
Convergence of random variables (and associated probability measures) comes in several modes: almost sure, Lp, in probability, but also in Wasserstein distance or Total Variation in the space of measures. [REF]

Harmonic function
2024-11-07
Harmonic functions solve Laplace's equation Δu = 0 and are infinitely differentiable (and analytic). They exhibit no local maxima or minima within the domain, achieving extrema only on the boundary. Under Dirichlet boundary conditions, Laplace solution is uniquely determined. [REF]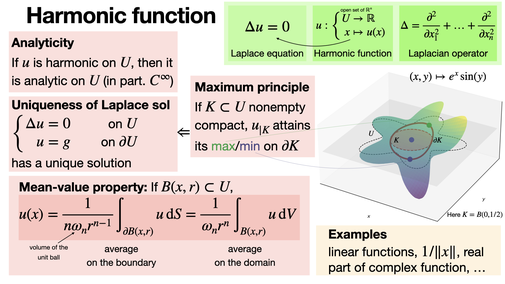
2024-11-07
Harmonic functions solve Laplace's equation Δu = 0 and are infinitely differentiable (and analytic). They exhibit no local maxima or minima within the domain, achieving extrema only on the boundary. Under Dirichlet boundary conditions, Laplace solution is uniquely determined. [REF]

Convolution and Fourier
2024-11-06
Convolution theorem: Fourier transform of the convolution of two functions (under suitable assumptions) is the product of the Fourier transforms of these two functions. [REF]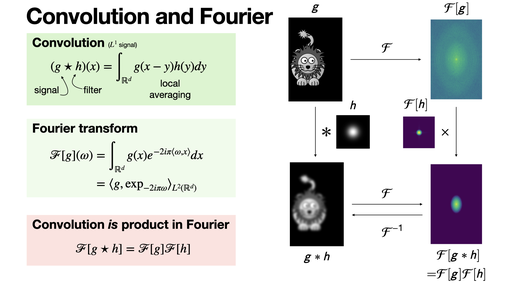
2024-11-06
Convolution theorem: Fourier transform of the convolution of two functions (under suitable assumptions) is the product of the Fourier transforms of these two functions. [REF]

Dual numbers
2024-11-05
Dual numbers correspond to the completion of the real line with an nilpotent element ε different from 0. It can be thought as a universal linearization of functions, or as the forward-mode of automatic differentiation. [REF]
2024-11-05
Dual numbers correspond to the completion of the real line with an nilpotent element ε different from 0. It can be thought as a universal linearization of functions, or as the forward-mode of automatic differentiation. [REF]

Convergence of iterative differentiation
2024-11-04
Convergence of iterates does not imply convergence of the derivatives. Nevertheless, Gilbert (1994) proposed an interversion limit-derivative theorem under strong assumption on the spectrum of the derivatives. [REF]
2024-11-04
Convergence of iterates does not imply convergence of the derivatives. Nevertheless, Gilbert (1994) proposed an interversion limit-derivative theorem under strong assumption on the spectrum of the derivatives. [REF]

Leader-follower games
2024-11-01
Leader-follower games, also known as Stackelberg games, are models in game theory where one player (the leader) makes a decision first, and the other player (the follower) responds, considering the leader’s action. This is one the first instance of bilevel optimization.
2024-11-01
Leader-follower games, also known as Stackelberg games, are models in game theory where one player (the leader) makes a decision first, and the other player (the follower) responds, considering the leader’s action. This is one the first instance of bilevel optimization.

Matrix mortality problem
2024-10-31
The Matrix Mortality Problem asks if a given set of square matrices can multiply to the zero matrix after a finite sequence of multiplications of elements. It is is undecidable for matrices of size 3x3 or larger. [REF]
2024-10-31
The Matrix Mortality Problem asks if a given set of square matrices can multiply to the zero matrix after a finite sequence of multiplications of elements. It is is undecidable for matrices of size 3x3 or larger. [REF]

Boolean satisfiability (SAT)
2024-10-30
The SAT problem asks whether a logical formula, composed of variables and (AND, OR, NOT), can be satisfied by assigning True to the variables. SAT is NP-complete along with 3-SAT, with clauses of three literals, while 2-SAT, is in P! [REF]
2024-10-30
The SAT problem asks whether a logical formula, composed of variables and (AND, OR, NOT), can be satisfied by assigning True to the variables. SAT is NP-complete along with 3-SAT, with clauses of three literals, while 2-SAT, is in P! [REF]

Krein—Milman theorem
2024-10-29
The Krein-Milman theorem states that any compact convex subset of a locally convex topological vector space is the closed convex hull of its extreme points. In particular, the set of extreme points of a nonempty compact convex set is nonempty. [REF]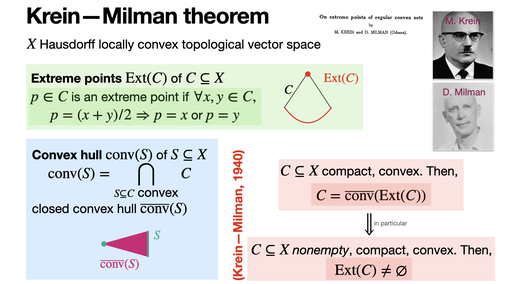
2024-10-29
The Krein-Milman theorem states that any compact convex subset of a locally convex topological vector space is the closed convex hull of its extreme points. In particular, the set of extreme points of a nonempty compact convex set is nonempty. [REF]

Stone-Weierstrass theorem
2024-10-28
The Stone-Weierstrass theorem states that any continuous function on a compact Hausdorff space can be uniformly approximated by elements of a subalgebra, provided the subalgebra separates points and contains constants. [REF]
2024-10-28
The Stone-Weierstrass theorem states that any continuous function on a compact Hausdorff space can be uniformly approximated by elements of a subalgebra, provided the subalgebra separates points and contains constants. [REF]

Nesterov Accelerated Gradient Descent
2024-10-25
The Nesterov Accelerated Gradient (NAG) algorithm refines gradient descent by using an extrapolation step before computing the gradient. It leads to faster convergence for smooth convex functions, achieving the optimal rate of O(1/k^2). [REF]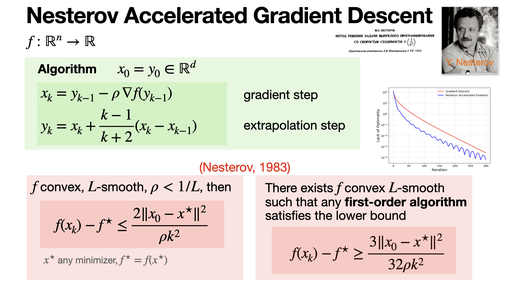
2024-10-25
The Nesterov Accelerated Gradient (NAG) algorithm refines gradient descent by using an extrapolation step before computing the gradient. It leads to faster convergence for smooth convex functions, achieving the optimal rate of O(1/k^2). [REF]

Pinhole camera model
2024-10-24
The pinhole camera model illustrates the concept of projective projection. Light rays from a 3D scene pass through an (infinitely) small aperture — the pinhole — and project onto a 2D surface, creating an inverted image on the focal plan. [REF]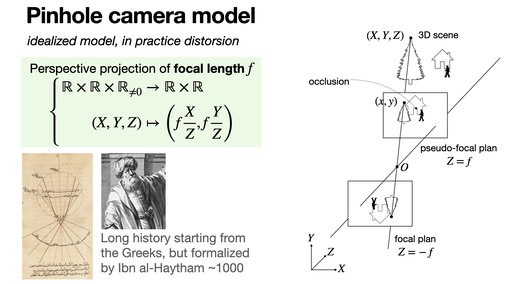
2024-10-24
The pinhole camera model illustrates the concept of projective projection. Light rays from a 3D scene pass through an (infinitely) small aperture — the pinhole — and project onto a 2D surface, creating an inverted image on the focal plan. [REF]

Łojasiewicz inequality
2024-10-23
Łojasiewicz inequality provides a way to control how close points are to the zeros of a real analytic function based on the value of the function itself. Extension of this result to semialgebraic or o-minimal functions exist. [REF]
2024-10-23
Łojasiewicz inequality provides a way to control how close points are to the zeros of a real analytic function based on the value of the function itself. Extension of this result to semialgebraic or o-minimal functions exist. [REF]

0x5F3759DF
2024-10-22
The fast inverse square root trick from Quake III is an algorithm to quickly approximate 1/√x, crucial for 3D graphics (normalisation). It uses bit-level manipulation and Newton's method for refinement. [REF]
2024-10-22
The fast inverse square root trick from Quake III is an algorithm to quickly approximate 1/√x, crucial for 3D graphics (normalisation). It uses bit-level manipulation and Newton's method for refinement. [REF]

Monge problem: existence? uniqueness?
2024-10-21
A Monge map, i.e., a solution to optimal transport Monge problems, may not always exist, be unique, or be symmetric with respect to the source and target distributions. It was one of the motivation to introduce Kantorovich relaxation. [REF]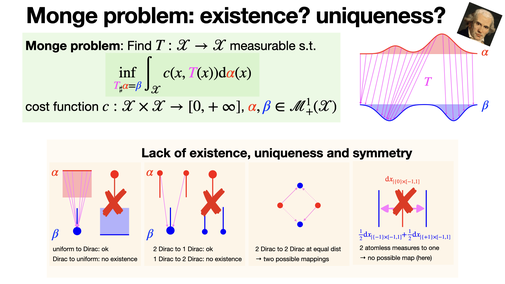
2024-10-21
A Monge map, i.e., a solution to optimal transport Monge problems, may not always exist, be unique, or be symmetric with respect to the source and target distributions. It was one of the motivation to introduce Kantorovich relaxation. [REF]

Attouch's theorem
2024-10-18
Attouch’ theorem relates the (epi-) convergence of convex lsc functions to the convergence of their subdifferential seen as graph on the product between the space and its dual. [REF]
2024-10-18
Attouch’ theorem relates the (epi-) convergence of convex lsc functions to the convergence of their subdifferential seen as graph on the product between the space and its dual. [REF]

Brenier's theorem
2024-10-17
Brenier's theorem states that the optimal transport map between two probability measures for quadratic cost is the gradient of a convex function. Moreover, it is uniquely defined up to a Lebesgue negligible set. [REF]
2024-10-17
Brenier's theorem states that the optimal transport map between two probability measures for quadratic cost is the gradient of a convex function. Moreover, it is uniquely defined up to a Lebesgue negligible set. [REF]

Weierstrass function
2024-10-16
The Weierstrass function is a famous example of a continuous function that is nowhere differentiable. It defies intuition by being continuous everywhere but having no tangent at any point. Introduced by Karl Weierstrass in 1872.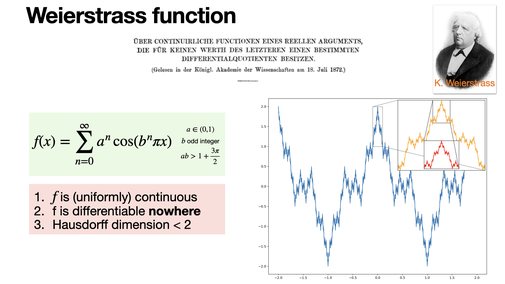
2024-10-16
The Weierstrass function is a famous example of a continuous function that is nowhere differentiable. It defies intuition by being continuous everywhere but having no tangent at any point. Introduced by Karl Weierstrass in 1872.

Proximal operator
2024-10-15
The proximal operator generalizes projection in convex optimization. It converts minimisers to fixed points. It is at the core of nonsmooth splitting methods and was first introduced by Jean-Jacques Moreau in 1965. [REF]
2024-10-15
The proximal operator generalizes projection in convex optimization. It converts minimisers to fixed points. It is at the core of nonsmooth splitting methods and was first introduced by Jean-Jacques Moreau in 1965. [REF]

Berry—Esseen Theorem (i.i.d version)
2024-10-14
The Berry-Esseen theorem quantifies how fast the distribution of the sum of independent random variables converges to a normal distribution, as described by the Central Limit Theorem (CLT). It provides an upper bound depending on skewness and sample size. [REF]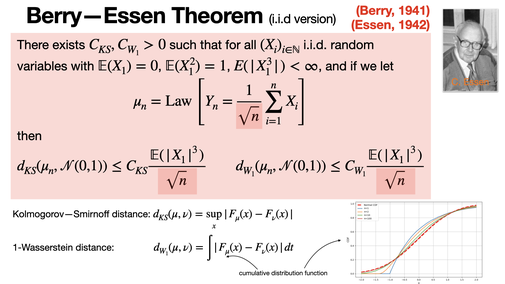
2024-10-14
The Berry-Esseen theorem quantifies how fast the distribution of the sum of independent random variables converges to a normal distribution, as described by the Central Limit Theorem (CLT). It provides an upper bound depending on skewness and sample size. [REF]

Bilevel Optimization: optimistic vs pessimistic
2024-10-11
Bilevel optimization problems with multiple inner solutions come typically in two flavors: optimistic and pessimistic. Optimistic assumes the inner problem selects the best solution for the outer objective, while pessimistic assumes the worst-case solution is chosen.
2024-10-11
Bilevel optimization problems with multiple inner solutions come typically in two flavors: optimistic and pessimistic. Optimistic assumes the inner problem selects the best solution for the outer objective, while pessimistic assumes the worst-case solution is chosen.

Geometry — according to Klein
2024-10-10
Klein geometry, part of the Erlangen Program introduced by F. Klein, studies geometry via transformation groups. A Klein geometry is defined as a space X=G/H, where G is a Lie group acting transitively on X. This unifies classical geometries under symmetry.[REF]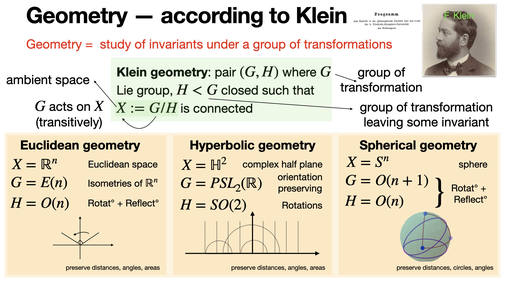
2024-10-10
Klein geometry, part of the Erlangen Program introduced by F. Klein, studies geometry via transformation groups. A Klein geometry is defined as a space X=G/H, where G is a Lie group acting transitively on X. This unifies classical geometries under symmetry.[REF]

Fenchel conjugate in 1D
2024-10-09
The Fenchel conjugate f*(y) is the maximum vertical gap between the line yx and the graph of f. This maximum occurs where the line is tangent to the curve, meaning f'(x) = y. It captures the largest gap at that tangent point.
2024-10-09
The Fenchel conjugate f*(y) is the maximum vertical gap between the line yx and the graph of f. This maximum occurs where the line is tangent to the curve, meaning f'(x) = y. It captures the largest gap at that tangent point.
Gradient conjecture of R. Thom
2024-10-08
The Thom gradient conjecture states that the trajectory of a gradient flow of a real-analytic function must converge such that the secant converge also. It was proved by Kurdyka, Mostowski, and Parusiński in 2000. [REF]
2024-10-08
The Thom gradient conjecture states that the trajectory of a gradient flow of a real-analytic function must converge such that the secant converge also. It was proved by Kurdyka, Mostowski, and Parusiński in 2000. [REF]
Johnson–Lindenstrauss lemma (1984)
2024-10-07
The Johnson–Lindenstrauss Lemma states that a set of high-dimensional points can be mapped into a much lower-dimensional space while approximately preserving pairwise distances. This is useful for dimensionality reduction, clustering, etc. [REF]
2024-10-07
The Johnson–Lindenstrauss Lemma states that a set of high-dimensional points can be mapped into a much lower-dimensional space while approximately preserving pairwise distances. This is useful for dimensionality reduction, clustering, etc. [REF]

Stein's lemma
2024-10-04
Stein's Lemma states that for a normally distributed variable X, the expected value E[Xg(X)] = E[g’(X)] for any g absolutely continuous (derivative a.e.) such that E[|g’(X)|] < ∞. It is a central result for characterizing (close-to) Gaussian data [REF]
2024-10-04
Stein's Lemma states that for a normally distributed variable X, the expected value E[Xg(X)] = E[g’(X)] for any g absolutely continuous (derivative a.e.) such that E[|g’(X)|] < ∞. It is a central result for characterizing (close-to) Gaussian data [REF]

Erdős–Rényi(–Gilbert) graph models
2024-10-03
Erdős–Rényi-Gilbert graph models are two random models introduced in 1959 sharing a lot of common properties. In particular, G(n, p) exhibits a sharp threshold for the connectedness for p ≈ n/ln n. [REF]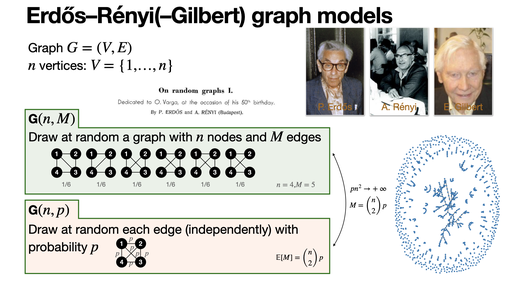
2024-10-03
Erdős–Rényi-Gilbert graph models are two random models introduced in 1959 sharing a lot of common properties. In particular, G(n, p) exhibits a sharp threshold for the connectedness for p ≈ n/ln n. [REF]

Law(s) of Large Numbers
2024-10-02
The law of large numbers tells that the empirical mean of an integrable random sample converges towards its mean in probability (weak LLN) and almost surely (strong LLN). [REF]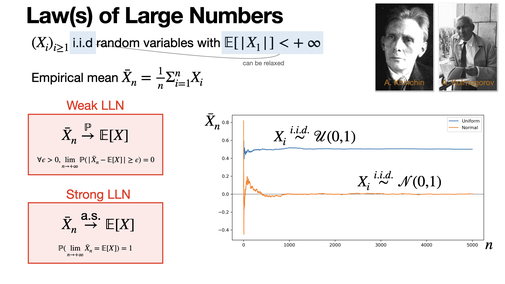
2024-10-02
The law of large numbers tells that the empirical mean of an integrable random sample converges towards its mean in probability (weak LLN) and almost surely (strong LLN). [REF]

Tarski—Seidenberg: logical statement
2024-10-01
The Tarski-Seidenberg theorem in logical form states that the set of first-order formulas over the real numbers is closed under quantifier elimination. This means any formula with quantifiers can be converted into an equivalent quantifier-free formula. [REF]
2024-10-01
The Tarski-Seidenberg theorem in logical form states that the set of first-order formulas over the real numbers is closed under quantifier elimination. This means any formula with quantifiers can be converted into an equivalent quantifier-free formula. [REF]

Davis—Kahan sin(θ) inequality
2024-09-30
The Davis-Kahan sin(θ) theorem bounds the difference between the subspaces spanned by eigenvectors of two symmetric matrices, based on the difference between the matrices. It quantifies how small perturbations in a matrix affect its eigenvectors. [REF]
2024-09-30
The Davis-Kahan sin(θ) theorem bounds the difference between the subspaces spanned by eigenvectors of two symmetric matrices, based on the difference between the matrices. It quantifies how small perturbations in a matrix affect its eigenvectors. [REF]

Grid search
2024-09-27
Grid search is the most popular method for hyperparameter optimization in machine learning. Using a performance metric, it simply aims to “exhaustively” evaluate this metric on a discretisation of the sample space. It suffers from the curse of dimensionality.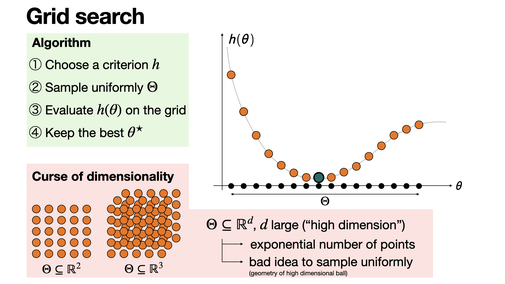
2024-09-27
Grid search is the most popular method for hyperparameter optimization in machine learning. Using a performance metric, it simply aims to “exhaustively” evaluate this metric on a discretisation of the sample space. It suffers from the curse of dimensionality.

Determinant vs Permanent
2024-09-26
The determinant and permanent of a matrix may look similar, but they differ fundamentally: the determinant includes the signatures of permutations, while the permanent uses only addition. One is easy to compute, the others expected to be very hard. [REF]
2024-09-26
The determinant and permanent of a matrix may look similar, but they differ fundamentally: the determinant includes the signatures of permutations, while the permanent uses only addition. One is easy to compute, the others expected to be very hard. [REF]

Chordal slope lemma
2024-09-25
If you pick three points along the curve in increasing order, the slope of the line between the first two points will always be less than or equal to the slope of the line between the last two points (chordal slope's lemma)
2024-09-25
If you pick three points along the curve in increasing order, the slope of the line between the first two points will always be less than or equal to the slope of the line between the last two points (chordal slope's lemma)
Finite-difference in 1D (forward)
2024-09-24
Finite difference approximation is a numerical method to compute derivatives by discretization. The forward difference illustrated here is a first order approximation of the order of the stepsize. [REF]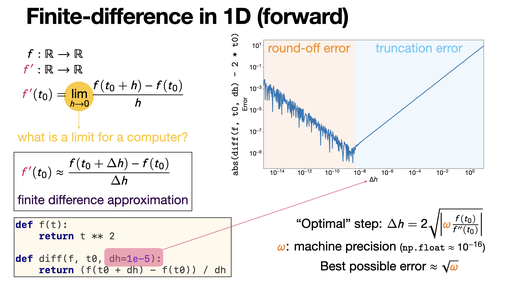
2024-09-24
Finite difference approximation is a numerical method to compute derivatives by discretization. The forward difference illustrated here is a first order approximation of the order of the stepsize. [REF]

Barycenters in the Wasserstein space
2024-09-23
Barycenters in the Wasserstein space were studied by Agueh & Carlier in 2011. They define meaningful geometric mean for probability distribution, and are used in practice for instance for histogram transfer (Rabin et al. ’15) [REF]
2024-09-23
Barycenters in the Wasserstein space were studied by Agueh & Carlier in 2011. They define meaningful geometric mean for probability distribution, and are used in practice for instance for histogram transfer (Rabin et al. ’15) [REF]
Tarski—Seidenberg: geometric statement
2024-09-20
Tarski—Seidenberg theorem claims that semialgebraic sets on 𝐑 are stable by projection. [REF]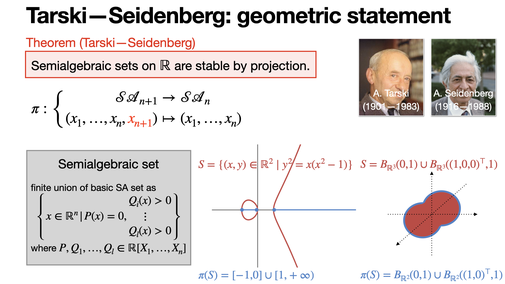
2024-09-20
Tarski—Seidenberg theorem claims that semialgebraic sets on 𝐑 are stable by projection. [REF]

Semialgebraic set
2024-09-19
Semialgebraic sets can be expressed as finite union of polynomial equalities and inequalities. [REF]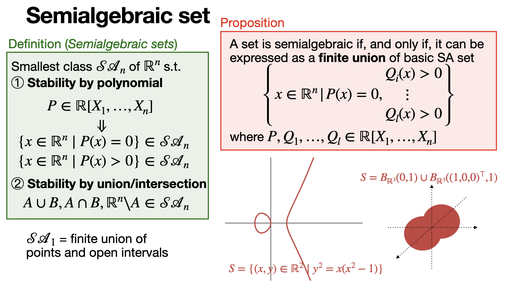
2024-09-19
Semialgebraic sets can be expressed as finite union of polynomial equalities and inequalities. [REF]

Banach fixed point & Picard’s iterations
2024-09-18
Banach fixed point theorem guarantees existence and uniqueness of fixed point of contraction mapping in metric spaces. It is at the root of the fixed point method.
2024-09-18
Banach fixed point theorem guarantees existence and uniqueness of fixed point of contraction mapping in metric spaces. It is at the root of the fixed point method.

Dual and polar cones
2024-09-17
Dual cone and polar cone are sets in the dual of a vector space. They generalize the notion of orthogonal subspace.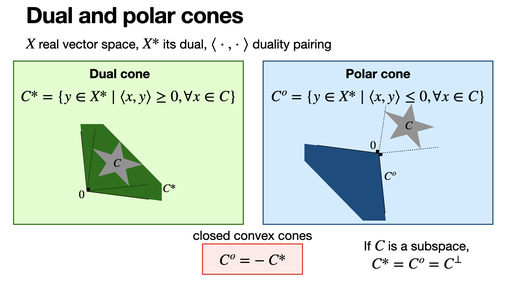
2024-09-17
Dual cone and polar cone are sets in the dual of a vector space. They generalize the notion of orthogonal subspace.

Voronoi diagram
2024-09-16
Voronoi diagram partitions the space in a proximity graph (cells) according to some sites. Each cell is the portion of the space where every points are closer to a given site than any other sites. [REF]
2024-09-16
Voronoi diagram partitions the space in a proximity graph (cells) according to some sites. Each cell is the portion of the space where every points are closer to a given site than any other sites. [REF]
Hamming distance
2024-09-13
Hamming distance is fundamental in coding theory: it corresponds to the number of different characters between two words of the same length. [REF]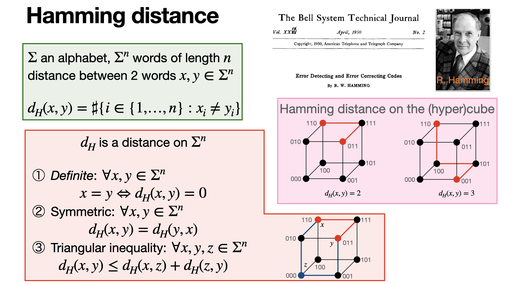
2024-09-13
Hamming distance is fundamental in coding theory: it corresponds to the number of different characters between two words of the same length. [REF]

The rendering equation
2024-09-12
The rendering equation is the fundamental recursive integral equation of light transport proposed by Kajiya in 1986, at the heart of (ray) path-tracing and particle tracing. Numerous sampling methods have been proposed to solve it numerically. [REF]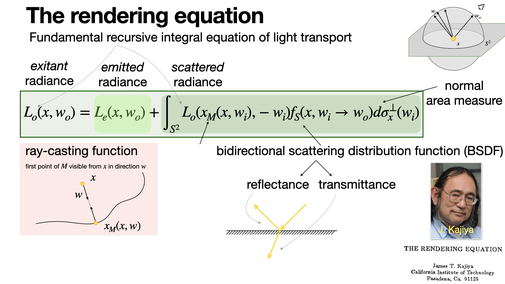
2024-09-12
The rendering equation is the fundamental recursive integral equation of light transport proposed by Kajiya in 1986, at the heart of (ray) path-tracing and particle tracing. Numerous sampling methods have been proposed to solve it numerically. [REF]

Random graph models
2024-09-11
Latent position models encompass popular random models of graphs such as SBM, Erdos-Renyi, etc. They are based on a latent space and a connectivity kernel, and strongly linked to graphons in the dense case. [REF]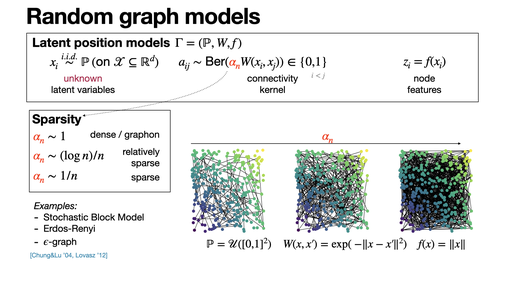
2024-09-11
Latent position models encompass popular random models of graphs such as SBM, Erdos-Renyi, etc. They are based on a latent space and a connectivity kernel, and strongly linked to graphons in the dense case. [REF]

Clarke Generalized derivative
2024-09-10
Clarke derivative generalizes the notion of convex subdifferential to nonconvex locally Lipschitz functions — thanks to Rademacher’s theorem — as the convex hull of the limiting sequences of gradient converging. [REF]
2024-09-10
Clarke derivative generalizes the notion of convex subdifferential to nonconvex locally Lipschitz functions — thanks to Rademacher’s theorem — as the convex hull of the limiting sequences of gradient converging. [REF]

Complex step approximation
2024-09-09
Complex step approximation is a numerical method to approximate the derivative from a single function evaluation using complex arithmetic. It is some kind of “poor man” automatic differentiation. [REF]
2024-09-09
Complex step approximation is a numerical method to approximate the derivative from a single function evaluation using complex arithmetic. It is some kind of “poor man” automatic differentiation. [REF]

Stochastic Block Model
2024-09-06
Stochastic block model is a popular generative model for graph proposed by Holland-Laskey-Leinhardt in 1983 to model communities. [REF]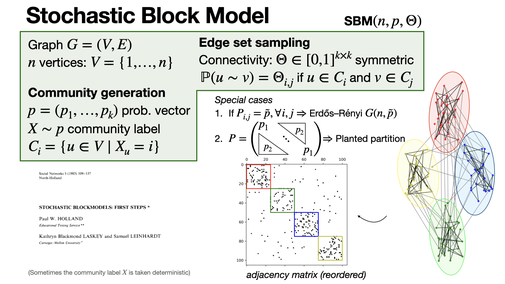
2024-09-06
Stochastic block model is a popular generative model for graph proposed by Holland-Laskey-Leinhardt in 1983 to model communities. [REF]

Thomae's popcorn & Dirichlet functions
2024-09-05
Thomae’s popcorn function is a (1-periodic) discontinuous function on ℚ but continuous on ℝ\ℚ that is nowhere differentiable. Dirichlet is nowhere continuous on ℝ. [REF]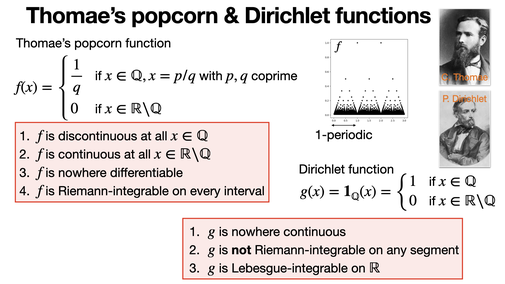
2024-09-05
Thomae’s popcorn function is a (1-periodic) discontinuous function on ℚ but continuous on ℝ\ℚ that is nowhere differentiable. Dirichlet is nowhere continuous on ℝ. [REF]

Weisfeiler-Leman test
2024-09-04
(1-dimensional) Weisfeiler-Leman is a heuristic for the graph isomorphism problem. It is a color refinement algorithm akin to a basic message passing scheme. [REF]
2024-09-04
(1-dimensional) Weisfeiler-Leman is a heuristic for the graph isomorphism problem. It is a color refinement algorithm akin to a basic message passing scheme. [REF]
Talagrand's inequality
2024-09-03
Talagrand's inequality is a probabilistic isoperimetric inequality that allows to derive a concentration inequality for the median. This is an instance of "concentration of measure" that made him win the Abel Prize in 2024. [REF]
2024-09-03
Talagrand's inequality is a probabilistic isoperimetric inequality that allows to derive a concentration inequality for the median. This is an instance of "concentration of measure" that made him win the Abel Prize in 2024. [REF]